On this page, I have attempted to compile a history of significant planetary N-body simulations. Historically, these simulations have focused on the solar system.

Moore’s Law, N-body simulations, and exoplanets

The number of known exoplanets has increased exponentially over the past couple decades at roughly the same time the growth in the clock rate of CPU cores has leveled off. N-body integrations are an essential part of exoplanet science– from fitting orbital parameters to observational data to simulating planet formation and evolution. The trend shown in the accompanying plot suggests that computational demands are quickly outstripping supply and new methods for handling the N-body dynamics of planetary systems are called for.

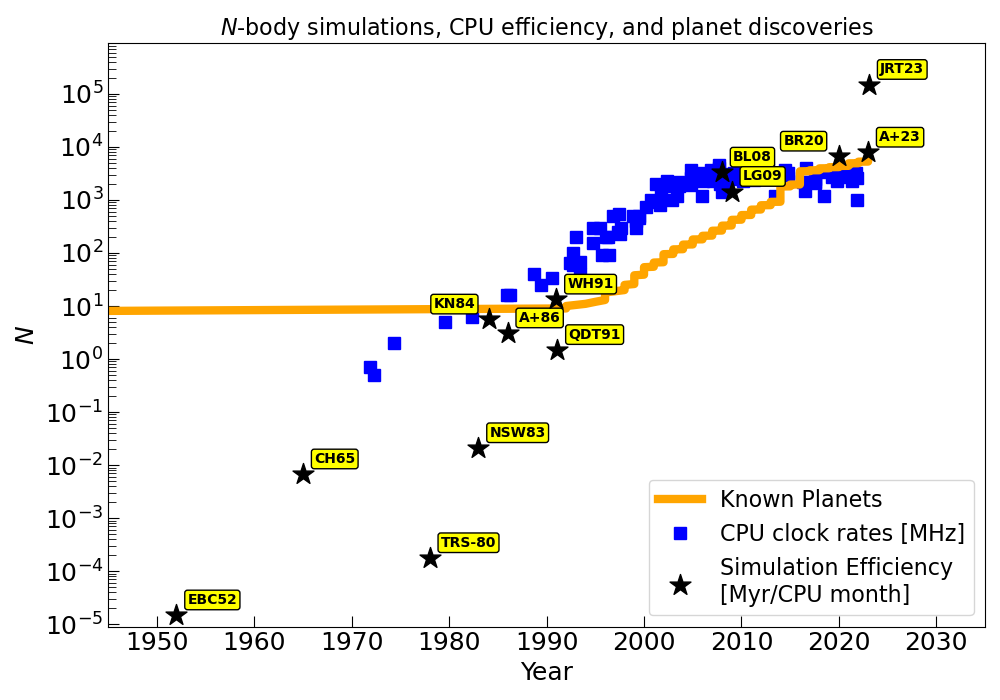
nbodyMoores

Data on exoplanet discoveries taken from the Exoplanet Archive. Data on CPU clock rates from Karl Rupp’s blog. Simulation efficiencies have are based on reported integration details and multiplied by (88 d./P_min)(N/8)^2 where P_min is the minumum orbital period among bodies included, Mercury’s orbital period is 88 days, and N is the number of bodies. In this way, I have attempted to account for variations between simulations in the bodies included (e.g., outer versus full solar system).

Notable N-body Simulations

  • EBC52: Eckert, Brouwer, and Clemenct (1952)
    • Outer solar system N-body integration spanning years 1653–2060
    • Simulation run on IMB’s SSEC for approx. 120 hours of compute time (thanks to Allan Olley for providing runtime estimate)
  • CH65: Cohen and Hubbard (1965)
    • 120 kyr integration of outer solar system
    • Revealed that that resonant librations protect Pluto from close encounter with Neptune
    • Cowell’s method with dt=40 day
    • 1500 yr per hour of compute time on the Naval Ordnance Research Calculator (NORC)
  • Cohen, Hubbard, and Oesterwinter (1973)
    • 1 Myr integration of outer solar system
    • Run on an IBM 7030
    • ORIGINAL REF??? (Linked paper only shows plots)
  • [TRS-80: Roger W. Sinnot]
  • NSW83: Newhall, Standish, and Williams (1983)
    • Integration of the entire solar system, as well as the moon, from 1411 BC to 3002 AD
    • 9 days of computer time to evaluate 6 million steps on a Univac 1100/81
  • KN84: Kinoshita and Nakai (1984)
    • 5 Myr integration of outer solar system
    • Störmer multi-step method with dt=40 day step size
    • 4 hour total run time on a FACOM380R
  • A+86:Digital Orrery (Applegate et. al. 1986)
    • 200 Myr integration of outer solar system
    • 12th order Störmer with dt=40 days
    • Special-purpose computer
      • Estimate a 1 yr run-time if performed on DEC VAX 11/780
      • Digital Orrery gives ~60x speed-up compared to DEC VAX 11/780
    • Estimate Lyapunov time of ~6 Myr for Pluto’s orbit
  • Sussman and Wisdom (1988)
    • Run on Digital Orrery computer
    • 845 Myr integration of the outer solar system
    • Numerical evidence for Pluto’s chaotic orbit
  • Project LONGSTOP (Roy et. al. 1988)
    • 100 Myr integration of outer solar system
    • suggested chaotic motion
    • Used a special multi-step Encke’s method with dt=40 days
    • Run on a CRAY-1S for RUNTIME???
  • QDT91: Quinn, Duncan, and Tremaine (1991)
    • 3 MYr integration of the entire solar system
    • Explicit multi-step methods
      • 12th order symmetric method
      • step size dt=0.75 day
    • 3 Myr integration run in 2 months of background time
    • No evidence of chaos
  • WH91: Wisdom and Holman (1991)
    • 1 Gyr integration of the outer solar system
    • 2nd-order symplectic Wisdom-Holman mapping method with dt=1 yr
    • 14 day runtime on a Hewlett-Packard HP9000/835 RISC workstation
  • BL08: Batygin and Laughlin (2008)
    • 20 Gyr integration of full solar system.
    • 2nd-order symplectic Wisdom-Holman mapping with dt=8 days
    • Applied ‘splitting’ method to demonstrate potential for Mercury instability
    • Run for approximately 6 months of CPU time (Batygin, private comm.)
  • LG09: Laskar and Gastineau (2009)
    • 5 Gyr integrations of entire solar sytem (ensemble of 2,501 integrations)
    • SABA4 symplectic integrator with dt=0.025 yr
    • Average run time of 2500 hours per 5 Gyr integration Xeon 5472 CPU cores
    • First direct N-body demonstrations of potential for Mercury orbital instabilities (with proper accounting for GR)
  • Abbot et. al. (2023)
    • Two 2,750-member ensembles of 5 Gyr simulations of entire solar system
    • Run with Wisdom-Holman algoirthm using dt=3.16 days
    • 2.5 million CPU-hours for entire set of simulations
  • JRT23: Javaheri, Rein, Tamayo (2023)
    • Implementation of the Wisdom-Holman algorithm that exploits SIMD parallelism and AVX512 instructions
    • Current record-holder for fastest solar system simulations